Cycle Scanner Framework
- Framework Overview
- Detrending
- Cycle Detection
- Cycle Validation
- Ranking
- Spectral Averaging
- Endpoint flattening
Framework Overview
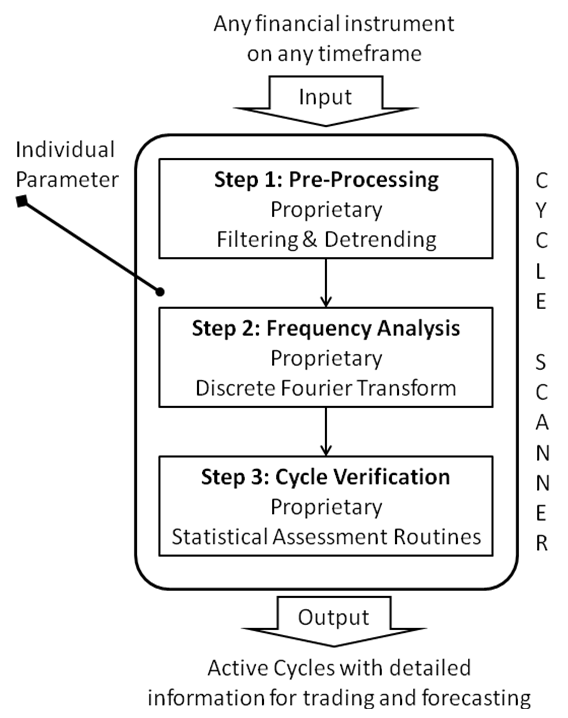
The following figure outlines how the Cycle Scanner algorithm works. The following pages describe each step of this algorithm.
Detrending
The algorithm has a dynamic filter for de-trending that is required for data preprocessing. Detrending ensures that the data under consideration is not affected by trends or one-time events. The extraction of linear trends in time series data is a required precondition for successful cycle research. In the business cycle literature, the Hodrick and Prescott (1980) filter (HP filter) has become the standard method for removing long-run movements, like trends, from the data. Hodrick and Prescott proposed the HP filter to decompose macroeconomic time series data into cycle and trend components. The HP filter assumes that movements in time series include a smooth and slowly changing trend component. By removing this trend component from the data series, the filter delivers the pure underlying cyclic behavior.
Visually, this de-trending technique is like drawing a smooth linear freehand trend line through the plotted chart data and extracting this "freehand" trend line from the full data set. The resulting component is only based on the cyclic behavior without the underlying trend. Now, we can proceed and start to apply additional cycle analysis in the next step to detect the cycles that are dominant and genuine within this filtered data set.
However, we must carefully treat the output obtained from this pure mechanical detrending algorithm because it is well-known that this technique may generate spurious cycle variants; that is, the HP filter can generate cycle dynamics even if none are present in the original data. Hence, the presence of cycles in HP-filtered data does not imply that real cycles exist in the original data. Therefore, we need to apply additional mechanisms to validate genuine identified cycles afterward and to remove possible "invalid" cycles. Later, at step 3 of our Cycle Scanner framework, we will show how to circumvent this problem by including goodness-of-fit statistics for our genuine dominant cycle filtering. [[1], [2] ]
To optimize the HP filter and to keep these shortcomings of spurious cycles as small as possible, first the proper adjustment of parameter "λ" in the decomposition of the HP filter is important.[[3]] Second, additional testing on how the estimated cyclical components behave based on cross-correlation evaluations are needed to differentiate “genuine” cycles from “spurious” ones. Both adjustments have been incorporated into our Cycle Scanner framework to compensate for the drawbacks of the HP filter.
A review of the critical discussions on the HP filter method, however, indicates that the HP filter is likely to remain the standard method for detrending for still a long time to come. Ravn and Uhlig concluded in 1997 as follows:
None of the shortcomings and undesirable properties are particularly compelling: the HP filter has withstood the test of the time and the fire of discussion remarkably well.
To further optimize the detrending preprocessing, additional recent findings based on the work of Jim Hamilton (2016) might be considered. [[4]]
However, the HP filter has broad support in the scientific area, and is widely used. We have been able to successfully use the approach for years in cycle forecasting: Never change a running system too fast. Therefore, we strongly recommend that anyone who wants to rebuild a similar or more optimized detrending framework should conduct further research in this area.
References
[1] Cogley, T., Nason, J. (1992): "Effects of the Hodrick-Prescott filter on trend and difference stationary time series: Implications for business cycle research," Journal of Economic Dynamics and Control.
[2] "Hodrick-Prescott Filter in Practice," Source: http://www.depeco.econo.unlp.edu.ar/jemi/1999/trabajo01.pdf
[3] Ravn, M., Uhlig, H. (1997): “On adjusting the HP-Filter for the Frequency of Observations.”
[4] James D. Hamilton (2016): “Why You Should Never Use the Hodrick-Prescott Filter,” Department of Economics, UC San Diego. Source http://econweb.ucsd.edu/~jhamilto/hp.pdf
Cycle Detection
As we now have the cyclical data set prepared, the next step is to discover the individual cycles that are active. Subsequently, the engine needs to perform a spectral analysis and then isolate those cycles that are repetitive and have the largest amplitudes. For that, we need to decide on a cycle detection algorithm that suits our goal. Most cycle researchers are familiar with the fast Fourier transform (FFT) and many "FFT-based engines" are available to detect one or more cycles in data sets. What many do not know, however, is that there is a special subset: the Goertzel algorithm [1] [2].
Originally, the algorithm was used to detect "dominant" tone frequencies used in landline phones for DTMF signaling, which was originally developed in 1958, long before the period of smartphones. Have you ever thought about how the telephone exchange knows what button has been pressed? The answer is the Goertzel algorithm. Today, the Goertzel algorithm is used extensively in communications for tone detection and is built into hardware as integrated circuits to detect tones of a button pushed in near-real-time.
Additionally, and even more important, the Goertzel algorithm was originally designed to detect cycles in data sets that have similar characteristics to contemporary financial series data. The problem a long time ago was that a special tone needed to be detected in a very short amount of available data and with considerable noise. This is similar to the problem of determining dominant cycles in financial data sets observed today.
Therefore, instead of using standard Fourier or wavelet transforms, why not use a well-established variant of the discrete Fourier transform (DFT): the Goertzel algorithm? As our requirements for cycle detection in financial markets are similar to the ones Goertzel was addressing in the case of old phone lines?
Our research shows that the Goertzel algorithm delivers reliable results in decoding dominant cycles out of detrended financial data sets, outperforming other methods such as wavelets or MESA.
For sure, you need to apply the Goertzel DFT (GDFT) in a special way, as you need to apply a GDFT test on all possible wavelengths and use different methods to obtain the current phase and amplitude. That is, for covering a full cycle length spectrum, the Goertzel algorithm has a higher complexity than FFT algorithms. Nevertheless, using the Goertzel algorithm to obtain the dominant cycle length out of short and noisy data, along with standard versions to obtain the related current phase and amplitude for the detected cycle length, helps generate all dynamic cycle data for the active cycle at the last point of our data set under consideration. As we are not interested in the “averaged” cycle length for longer data sets, we want the cycle length and phase that are active on the last bar of the chart. Therefore, this combination of the Goertzel algorithm as the core, with additional analysis to obtain the current phase of the cycle at the end of the data set, is used.
Finally, this approach is supported by a study conducted by Dennis Meyers (2003) on the Goertzel method: [3]
With very noisy data where the noise strength is greater than the signal strength, [...], only the Goertzel Algorithm can successfully identify the frequencies present.
In addition, we can see an increasing amount of noise coming into play for financial markets. Some examples of this are high-frequency trading, pure algo-based trading engines, or alternative news. So, in our real-life environments, we will not see a "clean" financial data set as it is diluted by noise that hides the real underlying cycles. The Meyers study shows that the GDFT even outperforms the proposed method "MESA" used by John F. Ehlers in most of his cycle research.
Therefore, our cycle scanner framework applies the GDFT to the detrended data set to cover all possible cycle lengths. Once the most active cycle is detected based on the full spectrum GDFT analysis, we use an additional run to check for the least current phase status on the last bar of our data set with a shorter subset of the original full data set, as we are interested in the status of the detected cycle length at the point of the analysis, or the last bar available.
References:
[1] Goertzel: https://www.mstarlabs.com/dsp/goertzel/goertzel.html
[2] Goertzel: https://courses.cs.washington.edu/courses/cse466/12au/calendar/Goertzel-EETimes.pdf
[3] Source: http://meyersanalytics.com/publications2/MesaVsGDFT.pdf
Cycle Validation
After finishing cycle analysis, we will get a list of detected active cycles. The cycle detection algorithm gave us a list of cycles with length, amplitude, and current phase status at the end of the data set. Now, we need to validate and rank these cycles as our approach is looking for the most active cycles out of this list.
Before we start to do some ranking, let us get back to what we introduced already in first detrending step: Based on the pitfalls of the HP-filter, we need to cross-check the detected cycles by using a second algorithm to validate if a cycle is genuine or perhaps spurious. So, this step is important to avoid getting "virtual" cycles that are not in the original data set and have just been returned by the detrending algorithm itself. Therefore, we apply a special form of statistical correlation analysis for each detected cycle length.
During this step of cycle validation, the statistical reliability of each cycle is evaluated. The goal of the algorithm is to exclude cycles that have been influenced by one-time random events (news, for example) and cycles that are not genuine.
One of the algorithms used for this purpose is a more sophisticated Bartels Test. The test builds on detailed mathematics (statistics) and measures the stability of the amplitude and phase of each cycle.
Bartels’ statistical test for periodicity, published at the Carnegie Institution of Washington in 1932, was embraced by the Foundation for the Study of Cycles decades ago as the single best test for a given cycle's projected reliability, robustness, and consequently, usefulness.
It was originally published in 1935 by Julius Bartels in Volume 40 No. 1 of the scientific magazine "Terrestrial Magnetism and Atmospheric Electricity" with the title "Random fluctuations, Persistence, and quasi-persistence in geophysical and cosmical periodicities." Later, Charles E. Armstrong gave a brief example and case study on how to apply the Bartels test in financial time series data in 1973, titled "Applying the Bartels Test of Significance to a Time Series Cycle Analysis." [1]
The Bartels test returns a value that gives the measure of the likelihood of genuineness of a cycle: values range from 0 up to 1, and the lower the value, the less likely is that this cycle is due to chance, or random.
The test considers both the consistency and the persistence of a given cycle within the data set it is applied to.
To make it more human readable as we are looking for an easily readable indication if the cycle is genuine, we just convert the raw Bartels value into a percentage that indicates how likely the cycle is genuine by using the conversion formula:
Cycle Score Genuine % = (1 - Bartels Score) * 100
It gives us a value between 0% (random) and 100% (genuine).
This test helps us now to filter out possible cycles that might have been detected in the cycle detection step (Step 2), but had only been in the data series for a short or random period and should therefore not be considered as dominant cycles in the underlying original data series.
As we have a final percentage score, we just need to define an individual threshold below which the cycles should be skipped. We recommend using a threshold of >49% and hence cycles with a Bartels genuine percentage value below 49% should be skipped by any cycle forecasting or analysis techniques that follow.
Further Reference:
[1] C. E. Armstrong, Cycles Magazine, October 1973, p. 231ff, "Part 25: Testing Cycles for Statistical Significance" (see pdf attachment)
Ranking
An important final step in making sense of the cyclic information is to establish a measurement for the strength of a cycle. Once ranking and sorting for detected cycles is completed, we have cycles that are dominant (based on their amplitude) and genuine (considering their driving force in the financial market). For trading purposes, this does not suffice. The price influence of a cycle per bar on the trading chart is the most crucial information.
Let me give you some examples by comparing two cycles. One cycle has a wavelength of 110 bars and an amplitude of 300. The other cycle has a wavelength of 60 bars and an amplitude of only 200.
So, if we apply the “standard” method for determining the dominant cycle, namely selecting the cycle with the highest amplitude, we would select the cycle with the wavelength of 110 and the amplitude of 300.
But let us look at the following information - the force of the cycle per bar:
- Length 110 / Amplitude 300 = Strength per bar: 300 / 110 = 2.7
- Length 60 / Amplitude 200 = Strength per bar: 200 / 60 = 3.3
For trading, it is more important to know which cycle has the biggest influence to drive the price per bar, and not only which cycle has the highest amplitude!
That is the reason I am introducing the measurement value “Cycle Strength.” The Cycle Scanner automatically calculates this value.
That said, to build a ranking based on the cycles left, we recommend sorting these cycles based on their "influence" per bar. As we are looking for the most dominant cycles, these are the cycles that influence the movement of the data-series the most per single bar.
Sort the outcome according to the calculated cycle strength score. Now we have a top-to-bottom list of cycles having the highest influence on price movements per bar.
What is the dominant cycle?
After the cycle scanner engine has completed all steps (detrend, detect, validate, rank), the cycle at the top of the list (with the highest cycle strength score) will provide us the information on the dominant cycle. In fact, the wavelength of this cycle is the dominant market vibration, which is very useful for cycle prediction and forecasting.
However, not only is the result limited to the cycle length (we not only have the dominant cycle length) but we also know—and this is very important—the current phase status of this cycle (Important: not the averaged phase over the full data set). This allows us to provide more valid cycle projections on the "right" side of the chart for trading instead of using the normally used "averaged" phase status over the full data set for this cycle.
Spectral Averaging
Cycles are not static, so what?
Most cycle analysts have seen the moment-to-moment fluctuations, often referred to as shifts in the length and phase of a cycle, which are common in continuous measurements of a supposedly steady spectrum of financial records. But wait, we should know that cycles are not static in real life. We can see these variations in size and phase for each cycle length in the updated spectrogram after a new data point/bar is added to the data set. Although small variations are certainly no cause for concern, we should remember that we do not live in an ideal, noise-free world, but we are always looking for ways to reduce the phase shifts and variations in dominant cycles.
Therefore, instead of additional smoothing of the input data, we will apply averaging to the received cycle spectrum. The basic idea of averaging to reduce spectral noise is the same as averaging - or smoothing - the input signal. However, touching the raw input signal with the averaging reduces data accuracy and results in a delay of the signal. This is not what we need, especially because the end of the data set - the current time - is of the utmost importance when working with cycles for financial time series data. Therefore, averaging the input and adding a delay to our series of interest is a bad idea for cycle analysis in data sets where the most recent current data points are more important than data points from long ago.
Dont smooth the input - average the spectrum!
Averaging a spectrum can reduce fluctuations in cycle measurements, making it an important part of spectrum measurements without changing the input signal or adding delay.
Spectral averaging offers a different approach and is a kind of ensemble averaging, meaning that the "sample" and "average" are both cycle spectra. The "average" spectrum is obtained by averaging the "sample" spectra. However, due to the nature of the spectra, this is not as simple as this. If you apply a discrete Fourier transform routine to a set of real-world samples to find a spectrum, the output is a set of complex numbers representing the magnitude and phase of that spectrum. Calculating an average spectrum involves averaging over common frequencies in several spectra.
Spectral averaging eliminates the effect of phase noise.
The size of the spectrum is independent of time shifts in the input signal, but the phase can change with each data set. By averaging the power spectra and taking the square root of the result, we eliminate the effect of phase variation. Reducing the noise variance helps us to distinguish small real cycles from the largest noisy peaks.
The result of spectral averaging is an estimate of the spectrum containing the same amount of energy as the source. Although the noise energy is preserved, the variance (noise fluctuation) in the spectrum is reduced. This reduction can help us reduce the detection of "false cycles" that are the result of single, one-time "noise" peaks. Lets illustrate the concept of spectral averaging with a simple example.
This method is a derivative of the so-called Bartlett method, if no other window than a rectangular window is applied to the data sections.
Cycle detection example
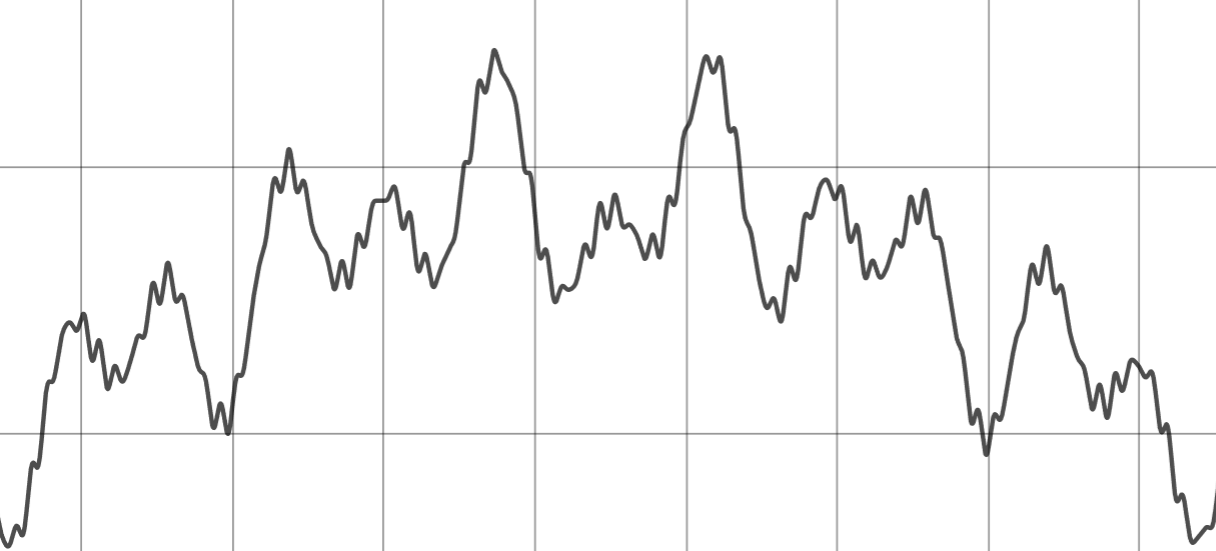
We use a constructed, simplified data-set which consists of 2 cycles, noise and different trends. The two cycles have a length of 45 and 80 days:
Raw input signal consisting of cycles, noise and trends
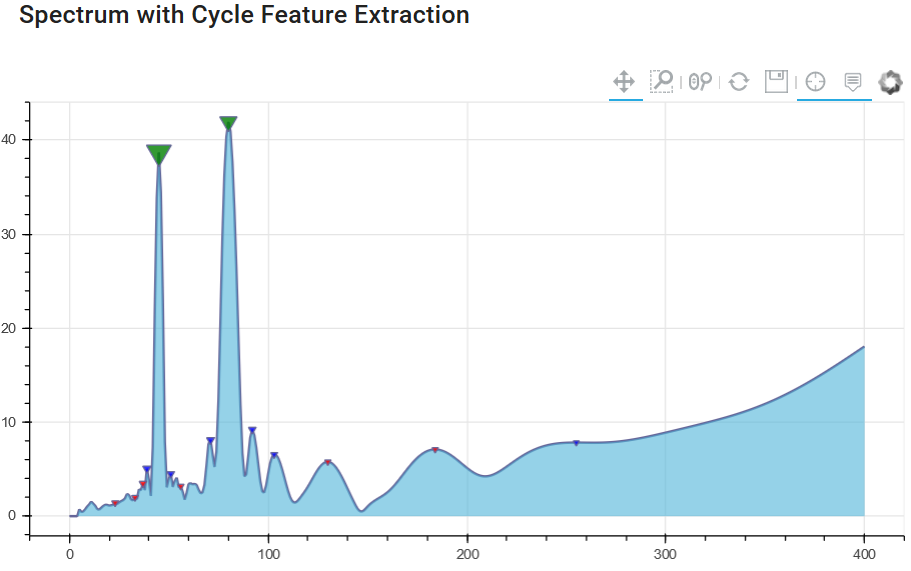
Let us have a look at the different spectrogram results without (1) and with (2) spectral averaging. The first diagram shows the basic amplitude spectrum of the signal without spectral averaging.
Chart 1: Cycle spectrum without spectrum averaging
It clearly shows the cycles with a amplitude peak at 45 and 80 days, but you can identify lower peaks in the spectrum that have nothing in common with real cycles of the original dataset. These smaller amplitude peaks are "false cycle" - noise only. We want to avoid using these cycles in cycle forecasting models.
Since it is important to identify and separate peaks based on noise - we will see if the method of averaging in the spectrum offers some added value. The next diagram uses the same input signal, but runs not just once to generate the spectrum, but several spectra to form the spectral average. In our case, the window only changes the beginning of the series and always uses the same end point for each spectrum.
This ensures that we have overlapping windows, always using the last available closer/bar and changing only the beginning of the series.
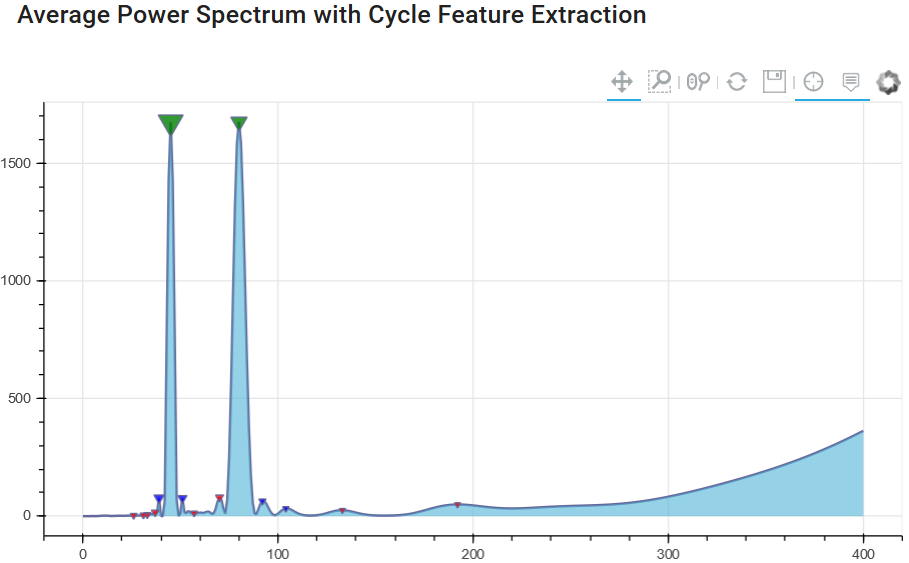
Chart 2: Cycle spectrum with spectrum averaging
The result illustrates that the peak values for 45 and 80 days are still present. But now the "noise" level has become much lower, and due to the averaging of the spectral window analysis, we have a lower number of "false cycle peaks". This will help us distinguish between important and unimportant cycles for future cycle prediction modeling techniques.
References:
- (2008) "The Spectral Analysis of Random Signals", in: Digital Signal Processing. Signals and Communication Technology. Springer, London. https://doi.org/10.1007/978-1-84800-119-0_7
- Oppenheim and Schafer (2009): "Discrete-Time Signal Processing", Chapter 10, Prentice Hall, 3rd edition.
- Bartlett (1950): "PERIODOGRAM ANALYSIS AND CONTINUOUS SPECTRA", Biometrika, Volume 37, Issue 1-2, June 1950, Pages 1–16, https://doi.org/10.1093/biomet/37.1-2.1
- Wikipedia: "Bartlett Method", https://en.wikipedia.org/wiki/Bartlett%27s_method
- Shearman (2018): "Take Control of Noise with Spectral Averaging", https://www.dsprelated.com/showarticle/1159.php
Endpoint flattening
The digital signal processing (e.g. Discrete Fourier Fransform) assumes that the time domain dataset is periodic and repeats.
Suppose a price series starts at 3200 and toggles and wobbles for 800 data samples and ends at the value 2400. The DFT assumes that the price series starts at zero, suddenly jumps to 3200, goes to 2400, and suddenly jumps back to zero and then repeats. The DFT has to create all sorts of different frequencies in the frequency domain to try to achieve this kind of behavior. These false frequencies, generated to match the jumps and the high average price, mask the amplitudes of the true frequencies and make them look like noise.
Fortunately, this effect can be nearly eliminated by a simple technique called endpoint flattening.
Example
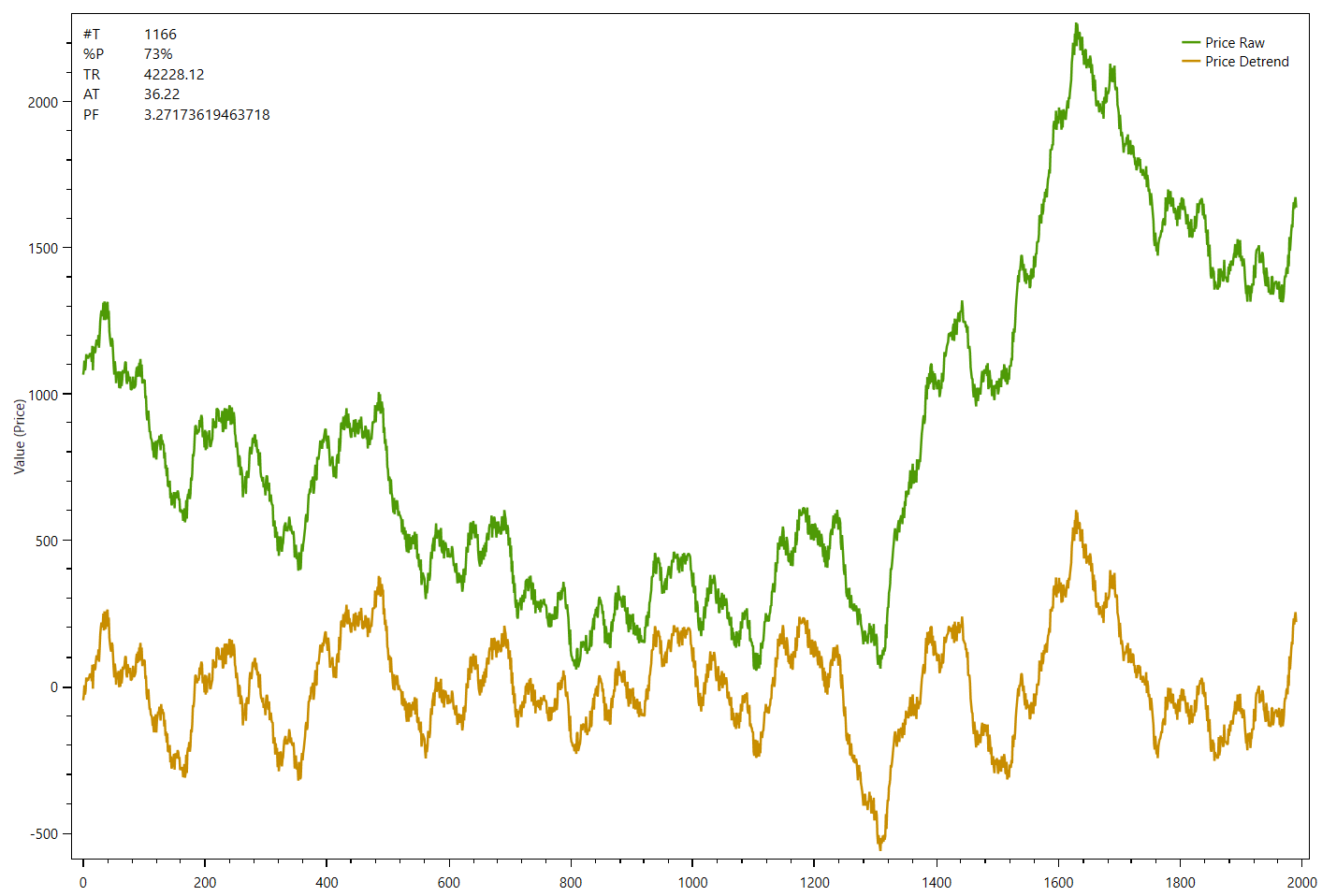
The following chart shows an example data series (green) and the de-trended data at the bottom panel (gold) without endpoint flattening:
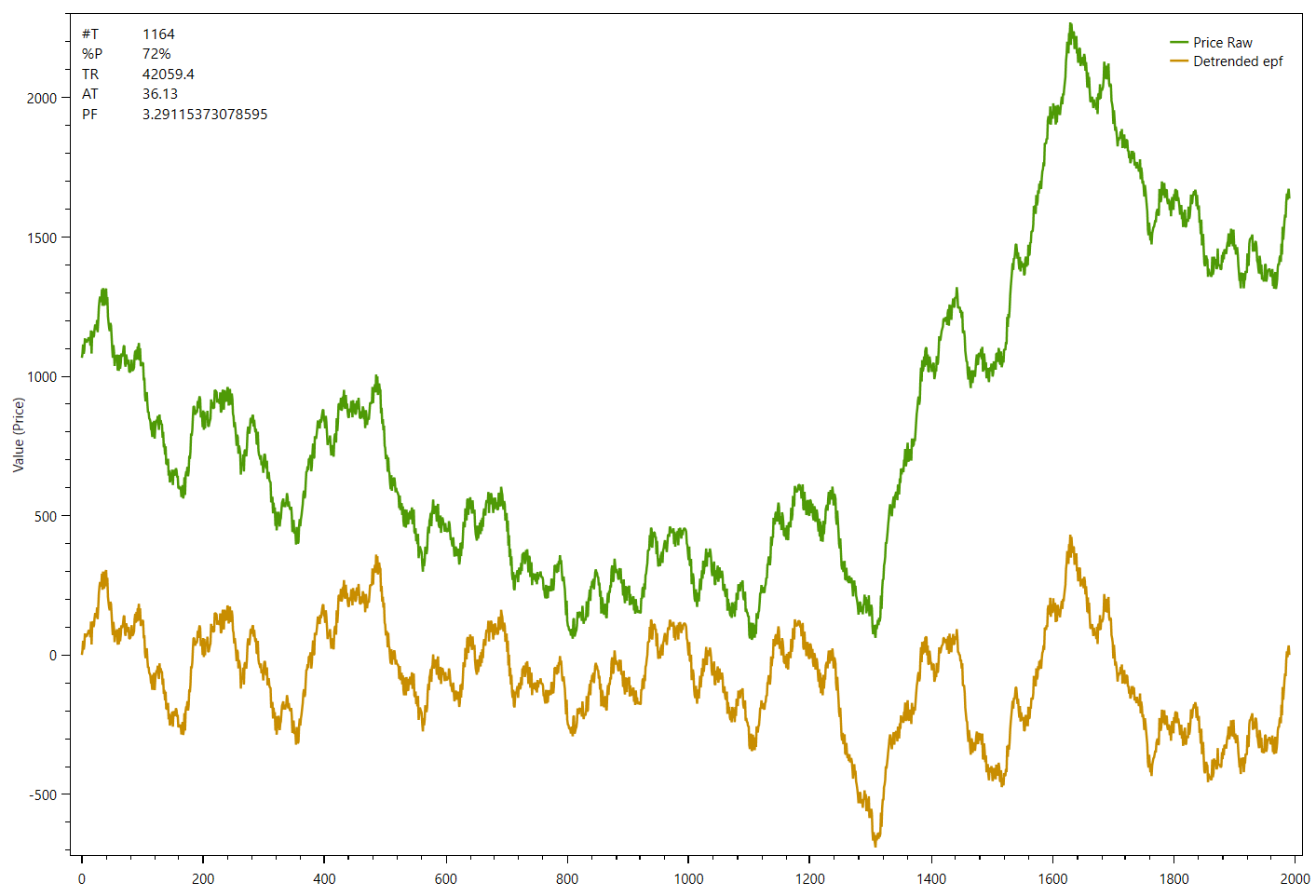
The next example shows the same data series now with endpoint flattening applied to the detrended series:
The difference is only visible at the beginning and the end on both de-trended series. While the first one starts below 0 and ends well above 0, the second chart shows that the de-trended series starts and ends at zero.
Math formula
Calculating the coefficients for endpoint flattening is simple:
Taking n closing prices. If x(1) represents the first price in the sampled data series, x(n) represents the last point in the data series, and xf(i) equals the new endpoint flattening series then:
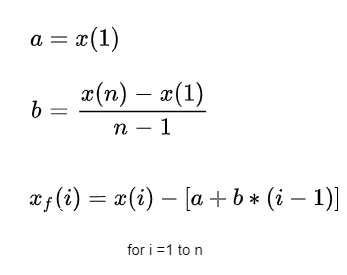
We can see that when i=1 then xf(1)=0 and when i=n then xf(n) =0.
What we’ve done is subtract the beginning value of the time series to make the first value equal to zero and then rotate the rest of the time series such that the end point is now zero. This technique reduces the endpoint distortion but introduces a low frequency artifact into the Fourier Frequency spectrum. Fortunately we won’t be looking for frequencies in that range so this distortion will have minimal impact.
C# .NET Function example
Apply end-point flattening to an array of double values:
public void endpointflattening(double[] values)
{
int datapoints = values.Count();
double a = values[0];
double xn = values[datapoints - 1];
double b = (xn - a) / (datapoints - 1);
for (int i = 0; i < datapoints; i++)
{
values[i] = values[i] - (a + (b * i));
}
}Further Reading & References: